SolutionShow Solution On a graph paper, draw a horizontal line X'OX and a vertical line YOY' as the xaxis and yaxis, respectively ∴ `y = (2x)/2` (i) Putting x = 2, we get y = 0 Putting x = 0, we get y = 1 Putting x = 2, we get y = 2 Thus, we have the following table for the equation x 2y 2 x = 7, y = 1 First, choose one of the 2 equations x 6y = 13 eq 1 2x 6y = 8 eq 2 For this answer i chose x 6y = 13 the first thing i'm going to do is to isolate the x, transfer 6y to the right side of the equal sign Then it becomes x = 13 6y eq 1 *noticed that 6y becomes negative when transferredSolve by Graphing xy=2 , xy=8, Subtract from both sides of the equation Multiply each term in by Tap for more steps Multiply each term in by Multiply Tap for more steps Multiply by Multiply by Simplify each term Tap for more steps Multiply by Multiply Tap for more steps
16 X Y 2 X Y 1 8 X Y 12 X Y 7 Find The Value Of X And Y Quora
X+y=8 x-y=2 graphical method
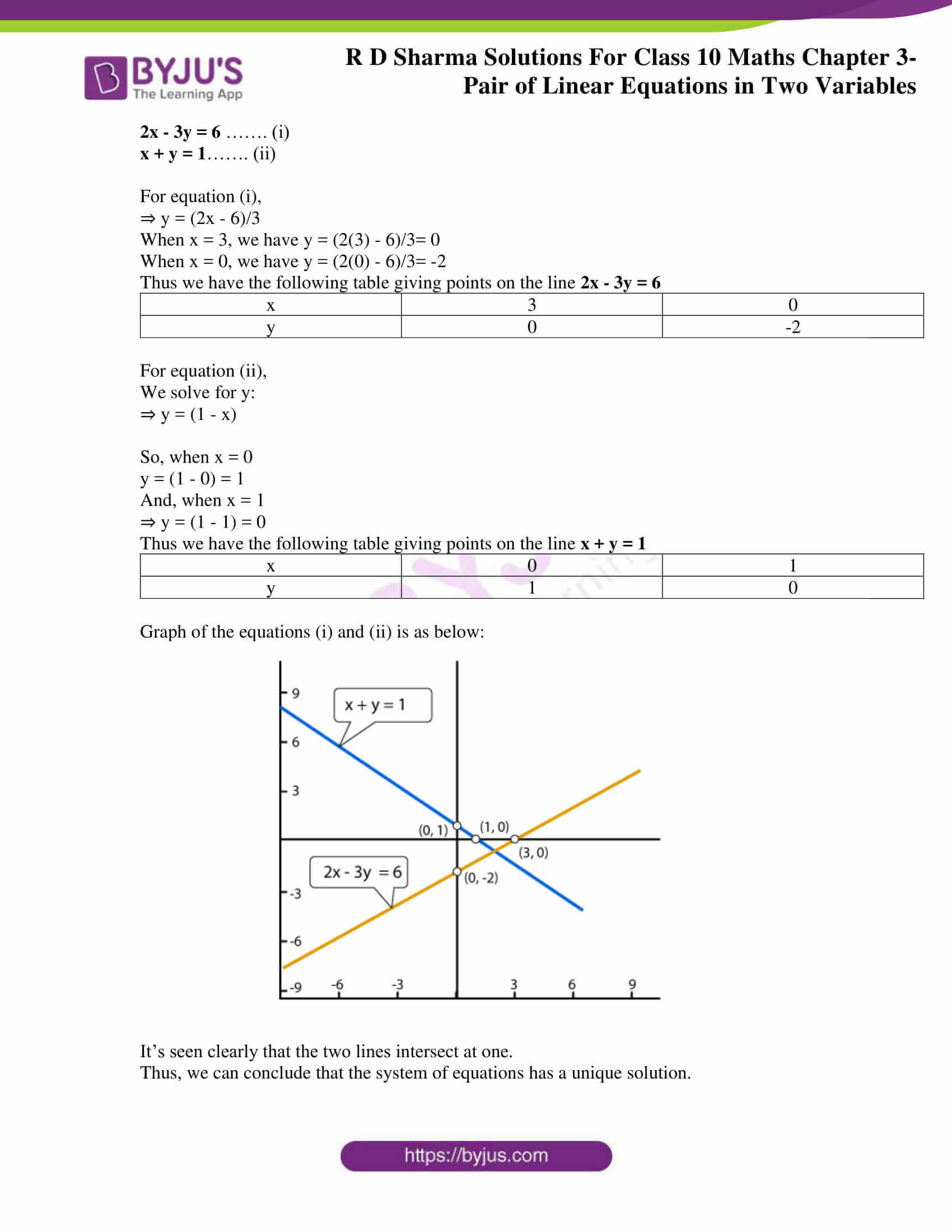
X+y=8 x-y=2 graphical method- Transcript Example 15 Solve the following system of inequalities graphically x 2y ≤ 8 , 2x y ≤ 8 , x ≥ 0 , y ≥ 0 First we solve x 2y ≤ 8 Lets first draw graph of x 2y = 8 Putting x = 0 in (1) 0 2y = 8 2y = 8 y = 8/2 y = 4 Putting y = 0 in (1) x 2(0) = 8 x 0 = 8 x = 8 Points to be plotted are (0,4) , (8,0) Drawing graph Checking for (0,0) Putting x = 0, y = 0 x 2y ≤ 3 Graphical Solution of a System of Linear Equations A `2 ×2` system of equations is a set of 2 equations in 2 unknowns which must be solved simultaneously (together) so that the solutions are true in both equations We can solve such a system of equations graphicallyThat is, we draw the graph of the 2 lines and see where the lines intersect




Graphing A Linear Equation 5x 2y Video Khan Academy
Draw the first three constraints, which are lines You'll get a shape with straight sides (two of which are the x and yaxes) and a certain number of corners, one of which is (0,0) I didn't actually graph those particular lines, so I don't knowX2 0 Goal produce a pair of x1 and x2 that (i) satis es all constraints and (ii) has the greatest objectivefunction valueType 1 Two Linear Graphs It is possible to solve linear simultaneous equations with graphs by finding where they intersect Example By plotting their graphs, for values of x between 1 and 4, on the same axes, find the solution to the two simultaneous equations below \begin{aligned}y&=2x5 \\ y&=x4\end{aligned}
3x y = 8 (i) 6x 2y = 16 (ii) Putting x = 0 in equation (i) we get `=> 3 xx 0 y = 8` `=> y = 8` x = 0, y = 8 Putting y = 0 in equations (i) we get `=> 3x 0 = 8` => x = 8/3 x = 8/3, y = 0 see below Graphically the roots are where the graph crosses the xaxis that is when y=0 graph{x^28x16 374, 1404, 256, 633} As can be seen from the graph it touches the xaxis at one point only x=4 Algebraically we could use factorising, completing the square or the formula look for factorising first x^28x=16=0 (x4)^2=(x4)(x4)=0 x4=0=>x=4 theVit C 2x y !
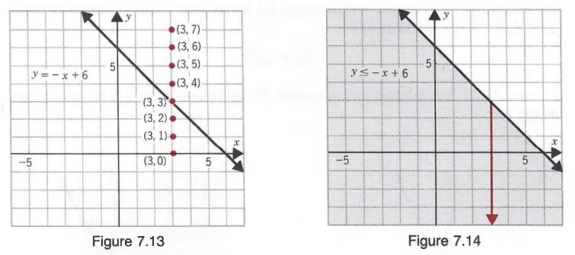
Now plot y = x/2 3 (as a solid line because y≤ includes equal to) 3 Shade the area below (because y is less than or equal to) Example y/2 2 > x 1 We will need to rearrange this one so "y" is on its own on the left Start with y/2 2 > x Subtract 2 from both sides y/2 > x − 2Solve the following pair of linear equations using Graphical method x y = 8;Observe that, given any values for x3 and x4, the values of x1 and x2 are determined uniquely by the equalities In fact, setting x 3 = x 4 = 0 immediately gives a feasible solution with x 1 = 6 and x 2
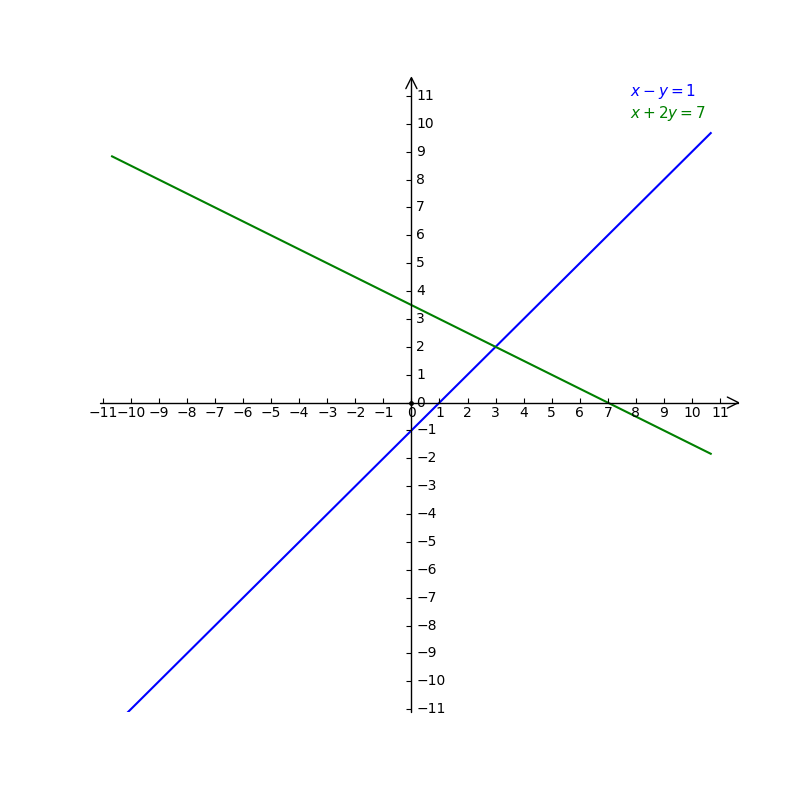



Solve The Simultaneous Linear Equations X Y 1 And Gauthmath




Solve Following Simultaneous Equation By Using Graphical Method X Y 8 X Y 2 Brainly In
#SahajAdhyayan #सहजअध्ययन #graphically Class 10 (इयत्ता 10वी ) Practice set 12 (सराव संच 12) Graphical Method x y = 0 ;SOLUTION xy=8;xy=2 simeltenious equations using graphical method Algebra > Graphs > SOLUTION xy=8;xy=2 simeltenious equations using graphical method Log On Algebra Graphs, graphing equations and inequalities Section8 iron 2x 2y !
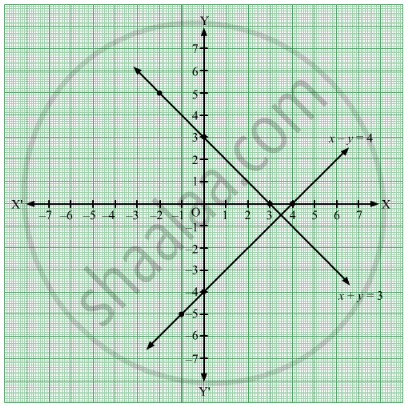



Complete The Following Table To Draw Graph Of The Equations I X Y 3 Ii X Y 4 Algebra Shaalaa Com



Solution X Y 8 X Y 2 Simeltenious Equations Using Graphical Method
Use graph paper for this question Take 2 cm = 2 units on xaxis and 2 cm = 1 unit on yaxis Solve graphically the following equations 3x 5y = 12;1 Using graphical method, solve the following linear programming problem Minimize T x y = 3 Subject to x 2y ≥ 4 x 3y ≥ 6 x ≥ 0 y ≥ 0 5 marks 2 A company needs to purchase a number of printing machines of which there are two types X and Y Type X costs shillings 000 and requires two operators and occupies 8 sq mtrs of floor spaceSolve the following pair of linear equations using Graphical method x y = 8;




Q3e 3x Y 10 X Y 2 Solve The Following Simultaneous Equation Graphically




Graphical Method Tilted Smith Charts In X Y Plane Download Scientific Diagram
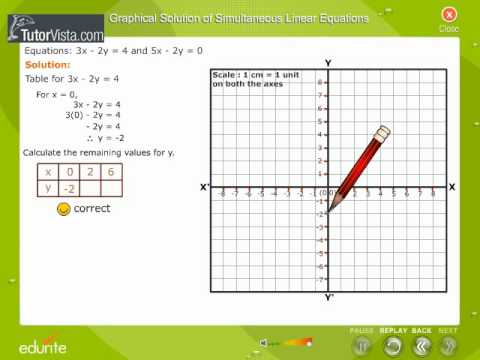
0 Cost = C = 4x3y The 3 blue lines are 48 = 4x3y 36 = 4x3y 24 = 4x3y The cost will be minimized if the strategy followed is the one corresponding to this corner point vit c x = #oz of A y = #oz of BThe simultanous equation calculator helps you find the value of unknown varriables of a system of linear, quadratic, or nonlinear equations for 2, 3,4 or 5 unknowns A system of 3 linear equations with 3 unknowns x,y,z is a classic example This solve linear equation solver 3 unknowns helps you solve such systems systematicallyTo find the yintercept (s), substitute in for and solve for Solve the equation Tap for more steps Remove parentheses Add and yintercept (s) in point form yintercept (s) yintercept (s) Create a table of the and values Graph the line using the slope and the yintercept, or the points




Equation Xy Yx Wikipedia
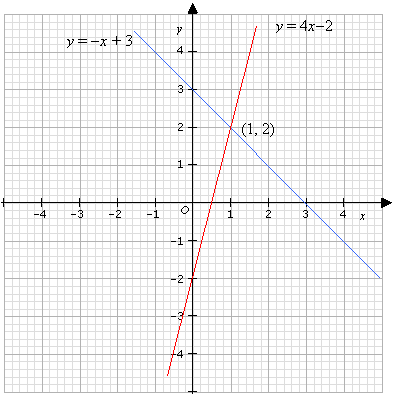



Systems Of Equations Graphical Method Video Lessons Examples Solutions
X y = 2 Then (x, y) is equal to 10th Maths Pair of Linear Equations in Two VariablesSolve for X and Y the equations are 2 X 3 Y is equal to 9 and 4 x 6 Y is equal to 15Thus, the line BC is the graph of 2x 3y = 2 Graph of x 2y = 8 x – 2y = 8 ⇒ 2y = (x – 8) ⇒ `y=(x8)/2` (ii) Putting x = 2, we get y = 3 Putting x = 4, we get y = 2 Putting x = 0, we get y = 4 Thus, we have the following table for the equation x – 2y = 8




X Y 8 X Y 2 Solution Of This Sum In Graphical Method Brainly In



Solve The Following Simultaneous Equations Graphically I 3x Y 2 0 2x Y 8 Ii 3x Y 10 X Y 2 Sarthaks Econnect Largest Online Education Community
Show that the lines y=3x7 and 2y6x=8 are parallel without using a graphical method Divide the equation of the second line, 2y6x=8, by 2This gives y3x=4Rearranging this so y is the subject gives the equation y=3x4These equations, y=3x7 and y=3x4, are in the form y=mxc, which is the general equation of a line, where m is the gradient ofWhen you have plotted the graphs, you can work out the values of \(x\) and \(y\) that solve the equations Example Use the graphical method to solve the simultaneous equations8) x will be 18, and y will be 8!
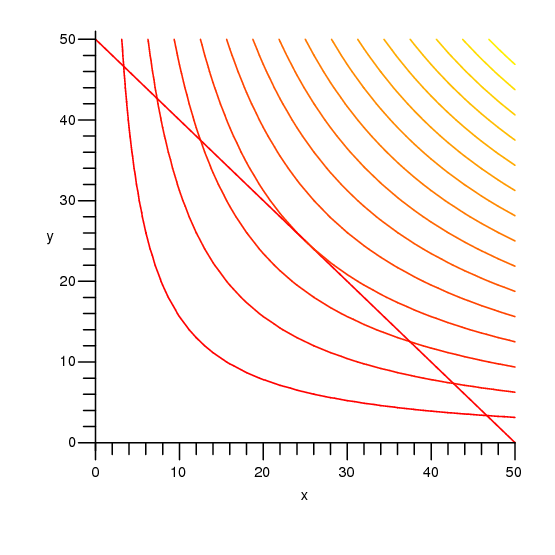



16 8 Lagrange Multipliers




Ex 6 3 8 Solve X Y 9 Y X X 0 Graphically Ex 6 3
Question 1 Using A Graphical Method, Maximise P = X 2y Subject To The Constraints ( 3x 4y = 8 X 4y = 16 3x 2y < 18 X, Y> 0 Note Use The Simplex Method To Solve Exercises 2 To 6 In Each Case, All Variables Are Nonnegative 2 Maximise P=3x 4y 3 Maximise P = 8x12y 102 Subject To 3x 2y = 15 Subject To 4x 3y 27 3 64 X Y = 10 2x Y Solve the following simultaneous equations by graphical method Complete the following tables to get ordered pairs x y = 1 5x 3y = 1 i Plot the above ordered pairs on the same coordinate plane ii Draw graphs of the equations iii Note the coordinates of the point of intersection of the two2 (x, y) (0, 8) (4, 0) (1, 6) (3, 2) The given lines intersect at (3, 2) ∴ x = 3 and y = 2 is the solution of the equations x – y = 1 and 2x y = 8 Concept Graphical Method of Solution of a




Graphical Method Of Solution Of A Pair Of Linear Equations Ck 12 Foundation
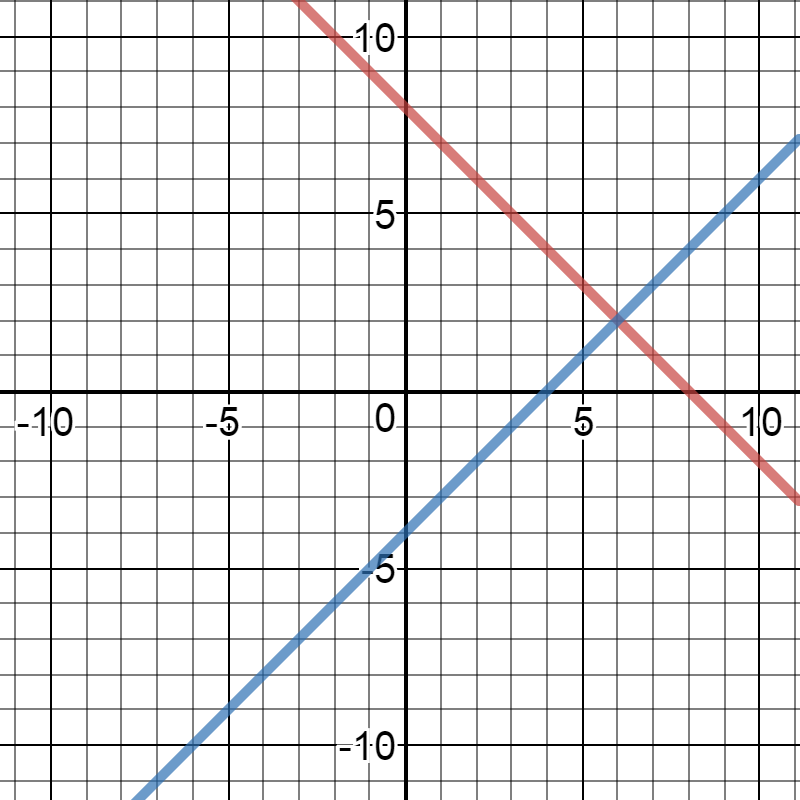



How Do You Solve The System Of Equations X Y 8 X Y 4 By Graphing Socratic
The solution is x=6, y=2 See explanation below To solve such a system you should regard each equation as a function of x and y, where x_1y_1=8, or y_1=x_18 To be able to plot the graph you will note that x=0 gives y=8, and y=0 gives x=8, so the two points (0, 8) and (8, 0) are on the line x_2y_2=4, or y_2=x_24 x=0 gives y=4, and y=0 gives x= 4, so this line must Transcript Ex 33, 1 Solve the following pair of linear equations by the substitution method (i) x y = 14 x – y = 4 x y = 14 x – y = 4 From equation (1) x y = 14 x = 14 – y Substituting value of x in equation (2) x – y = 4 (14 – y) – y = 4 14 – y – y = 4 14 – 2y = 4 –2y = 4 – 14 –2y = –10 y = (−10)/(−2) y = 5 Putting y = 5 in (2) x – y = 4 x = y 4 x The value of k for which the system of equations 2x3y=5 and 4xky=10 has infinite number of solutions, is What would be the graphical representation of the pair of linear equations 3x 5y = 9 and 6x 10y = 8?



3x Y 2 0 And 2x Y 8 Problem Set 1 Q3 4 Of Linear Equations In Two Variables Algebra Youtube
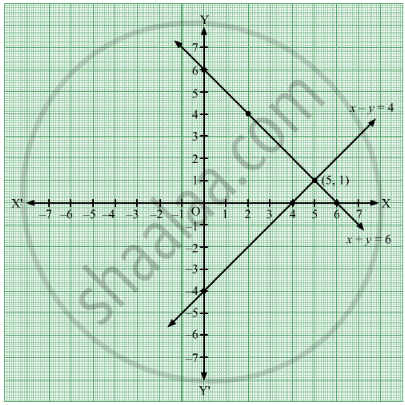



Solve The Following Simultaneous Equations Graphically X Y 6 X Y 4 Algebra Shaalaa Com
Solve the simultaneous equations by using Graphical method x 3y = 7;Find the optimal values of x and y using the graphical solution method Max 3x 2y subject to x ≤ 6 x y ≤ 8 2x y ≥ 8 2x 3y ≥ 12 Look at the point in which the 2 lines meet Get it's coordinates (x ;



26 Free Simultaneous Equations Worksheets And Lesson Plans For Ks3 And Ks4 Maths




Graphical Method Of Solution Of A Pair Of Linear Equations Ck 12 Foundation
Click here👆to get an answer to your question ️ Solve the following pair of linear equations using Graphical method x y = 8;Algebraic method You can solve simultaneous equations by adding or subtracting the two equations in order to end up with an equation with only one unknown value (x = 2\), \(y = 1\)The Graphical Simplex Method An Example Consider the following linear program Max 4x1 3x2 Subject to 2x1 3x2 6 (1) 3x1 2x2 3 (2) 2x2 5 (3) 2x1 x2 4 (4) x1;



Solve The Following Simultaneous Equations Graphically X Y 0 2x Y 9 Algebra Shaalaa Com



16 X Y 2 X Y 1 8 X Y 12 X Y 7 Find The Value Of X And Y Quora
2x y 1 = 0 PDF FILE TO YOUR EMAIL IMMEDIATELY PURCHASE NOTES & PAPER SOLUTION @ Rs 50/ each (GST extra) HINDI ENTIRE PAPER SOLUTION MARATHI PAPER SOLUTION SSC MATHS I3x 5y 18 = 0 (Plot only three points per line)Y) The x coordinate will be the value of x in the equation, and the y coordinate will be the value of y!
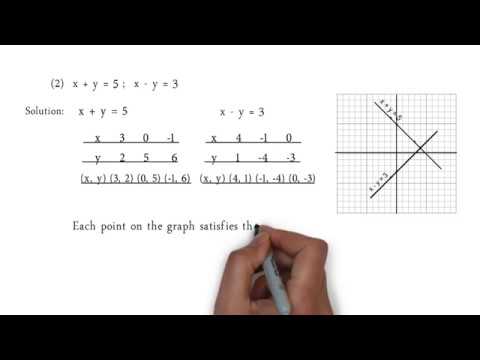



X Y 5 And X Y 3 P S 1 2 Q2 2 Linear Equations In Two Variables Youtube



Simultaneous Equations Graphically
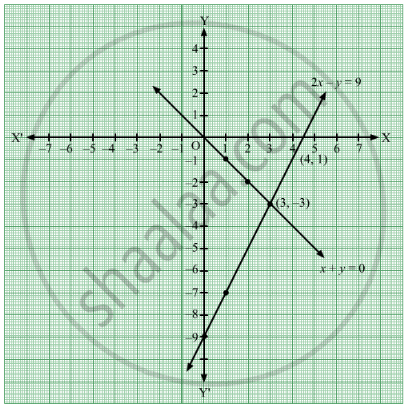
If you've been using the example, the lines should meet at point (18 ;Example Using the graphical method, find the solution of the systems of equations y x = 3 y = 4x 2 Solution Draw the two lines graphically and determine the point of intersection from the graph From the graph, the point of intersection is (1, 2)The graphical solution of the simultaneous equations is given by the point of intersection of the linear equations Consider x y = 8 xintercept When y = 0, x = 8 yintercept When x = 0, y = 8 Consider x – y = 2 xintercept When y = 0, x = 2 yintercept The diagram shows that the lines intersect at the point (5, 3) So, the



Rd Sharma Class 10 Solutions Maths Chapter 3 Pair Of Linear Equations In Two Variables Exercise 3 2



View Question X Y 2 And X Y 8
X − y = 2 Then ( x , y ) is equal toThe solution for the equation x 2 x – 3 can be obtained by looking at the points where the graph y = x 2 x – 3 cuts the xaxis (ie y = 0) The graph y = x 2 x – 3, cuts the xaxis at x 13 and x –23 So, the solution for the equation x x –3 is x 13 or x –23 Recall that in the quadratic formula, the discriminant b 2 – 4ac is positive when there are two distinct realMath 1313 Page 6 of 19 Section 21 Example 4 Use the graphical method to solve the following linear programming problem Maximize R x y= 4 11 subject to 3 2 4 0 0 x y x y x y ≤ ≤ ≥ ≥ Solution We need to graph the system of inequalities to produce the feasible set We will start
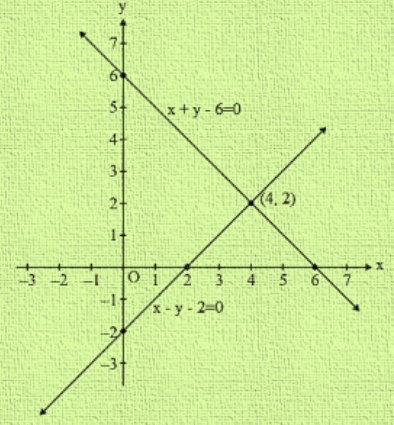



R D Sharma Class 10 Solutions Maths Chapter 3 Pair Of Linear Equations In Two Variables Exercise 3 2




Draw Graph For X Y 5 X Y 8 Brainly In
2x y = 8 x 0 4 y 8 0 The solution of the given equations is the point of intersection of the two line ie (2, 4) Concept Graphical Method of Solution of a Pair of Linear Equations2x y = 9 MarathiSolve using the Graphical method the following problem Maximize Z = f (x,y) = 3x 2y subject to 2x y ≤ 18 2x 3y ≤ 42 3x y ≤ 24 x ≥ 0 , y ≥ 0 Initially the coordinate system is drawn and each variable is associated to an axis (generally 'x' is associated to the horizontal axis and 'y' to the vertical one), as shown in




Graph Of An Equation




2x Y 8 X Y 1 Solve Graphically Brainly In
X y = 2 Then (x, y) is equal to Join / LoginPlot these graphs onto the axes and label each graph The point of intersection is (2, 3) which means \(x = 2\) and \(y = 3\) Solving linear and quadratic equations graphically HigherSimply graph each inequality and find the shaded area Now locate each of the vertices that fall on the border of this shaded area With each vertex, plug in the x and y coordinates into The pair of coordinates that maximize "z" will be the answer If what I'm saying doesn't help, then Start with the given system of inequalities



Graph Graph Equations With Step By Step Math Problem Solver




Omtex Classes X Y 8 X Y 2
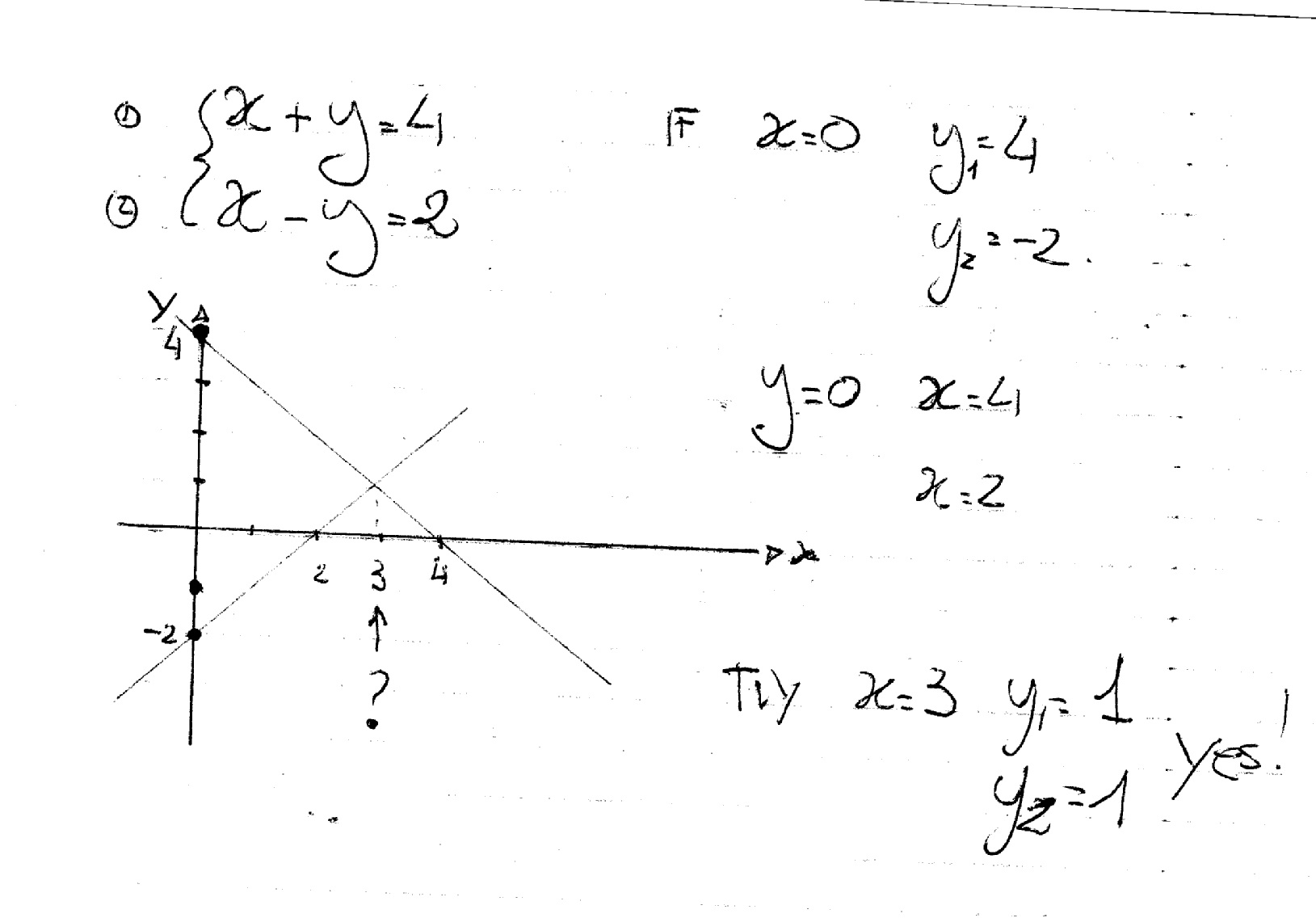
First graph the three functions that result from ignore de inequalities, taking it as equalities * 3x4y=18 > y=18/43x/4 * x4y=16 > y=4x/4 * 3x2y=18 > y=93xOf one of the letters is the same, regardless of sign Example Solve the following simultaneous equations \3x y = 11\ \2x y = 8\ First, identify which unknown has the same coefficientConsider the equation x y 7 and note that we can easily find many solutions For instance, if x = 5 then y 2, since 5 2 = 7 Also, if x = 3 then y = 4, since 3 4 = 7 If we represent these answers as ordered pairs (x,y), then we have (5,2) and (3,4) as two points on the plane that represent answers to the equation x y = 7




Solve The Following Simultaneous Equations X Y 8 X Y 2



How Do You Solve X Y 4 And X Y 2 By Graphing Socratic




System Of Equations Graphical Method



How Do You Solve The System Of Equations X Y 8 X Y 4 By Graphing Socratic



Graphical Solution Of Simultaneous Linear Equations Youtube




4 4 Solving Simultaneous Equations Equations And Inequalities Siyavula




Draw The Graphs Of The Equations X Y 1 A N D 2x Y 8 Shade The Area Bounded By These Two Lines And Y Axis Also Determine This Area



1



Solve The Following Simultaneous Equations Graphically I 3x Y 2 0 2x Y 8 Ii 3x Y 10 X Y 2 Sarthaks Econnect Largest Online Education Community



The Substitution Method




Implicit Differentiation




How To Solve Simultaneous Equations Graphically 8 Steps



3 Graphical Solution Of A System Of Linear Equations




Draw The Graph Of The Equations X Y 13 2x Y 8 Linear Equations In Two Variables Maths Class 9




Teaching X And Y Axis Graphing On Coordinate Grids Houghton Mifflin Harcourt
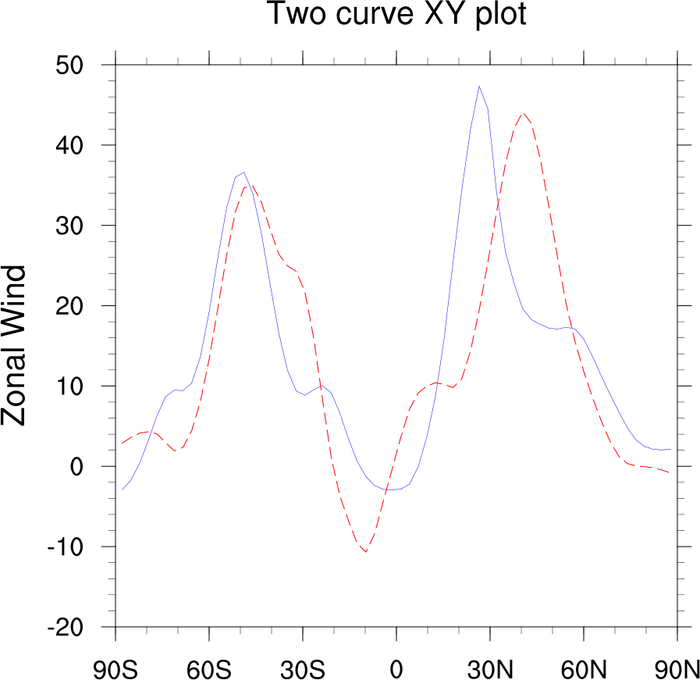



Ncl Graphics Xy



1



Simultaneous Equations Gmat Math Study Guide




Graphing Inequalities X Y Plane Review Article Khan Academy
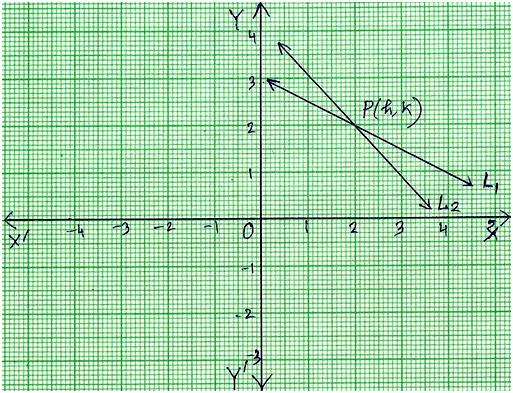



Simultaneous Equations Graphically Solve Graphically The System Of Equations
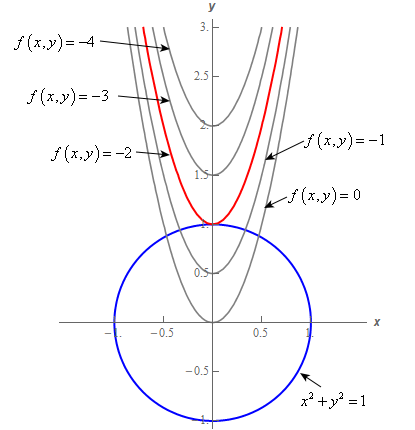



Calculus Iii Lagrange Multipliers




Graphing A Linear Equation 5x 2y Video Khan Academy




Graphical Method Of Solving Linear Equations In Two Variables A Plus Topper




4 4 Solving Simultaneous Equations Equations And Inequalities Siyavula




Ex 6 3 15 Solve Graphically X 2y 10 X Y 1
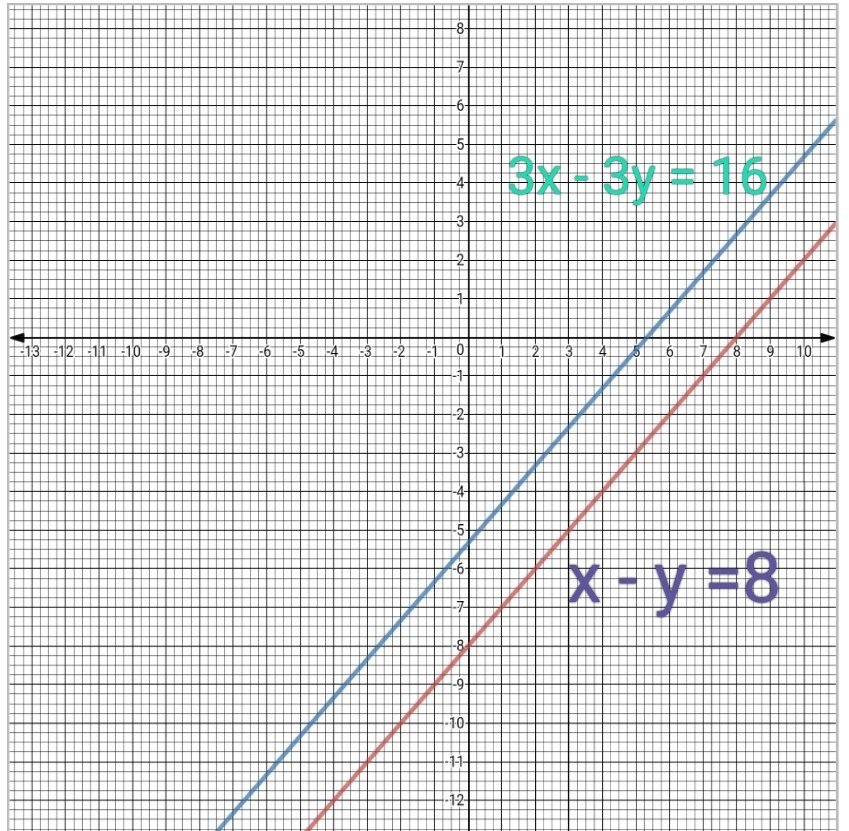



Show Graphically That The System Of Linear Equations X Y 8 3x 3y 16 Is Inconsistent I E It Has No Solution Snapsolve



16 X Y 2 X Y 1 8 X Y 12 X Y 7 Find The Value Of X And Y Quora




Graphical Method Of Solution Of A Pair Of Linear Equations Ck 12 Foundation




How To Solve Simultaneous Equations Graphically 8 Steps



Solve The Following Simultaneous Equations Graphically X Y 2 X Y 4



1
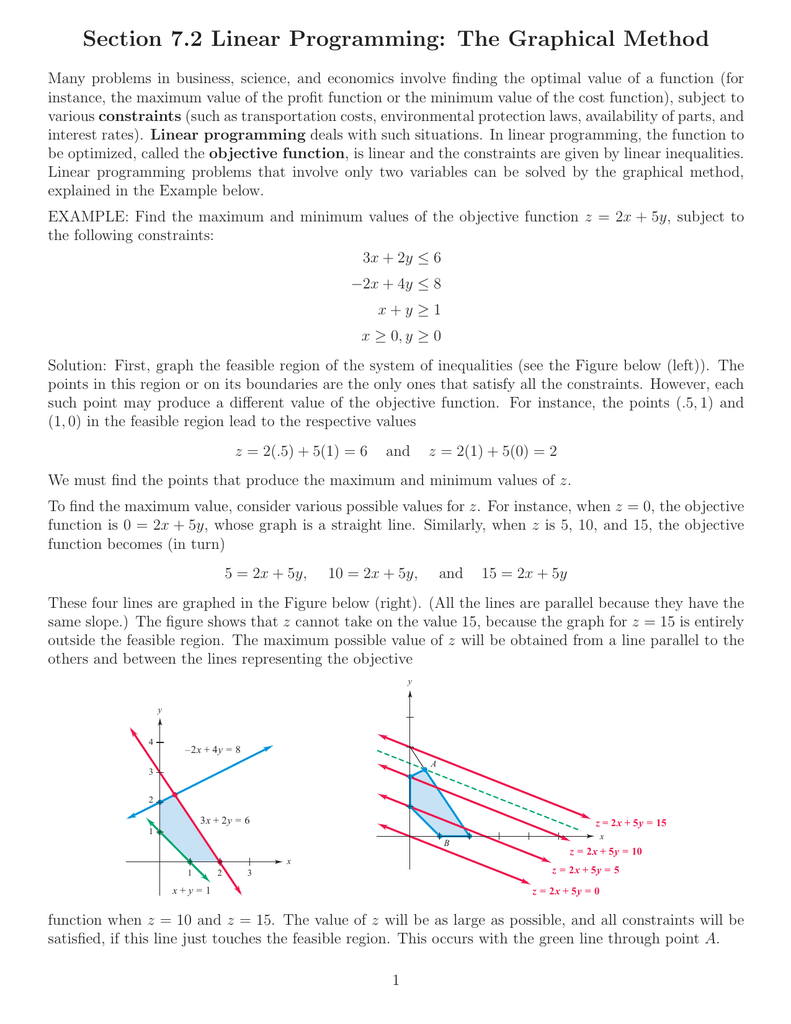



Section 7 2 Linear Programming The Graphical Method



Solving Systems Of Equations In Two Variables Algebra 2 How To Solve System Of Linear Equations Mathplanet




Draw The Graphs Of The Pair Of Linear Equations X Y 2 0 Amp 4x Y 4 0 Determine The Co Ordinates Of The Vertices Of The Triangle Formed By The Lines




Solve The Pair Of Linear Equation Graphically X Y 1 2x Y 8 Also Find Coordinateof Vertices Of The Triangle Formed By The Lines And Maths Meritnation Com



Systems Of Linear Equations



The Substitution Method



Q Tbn And9gcrjalofg0dijzc Pqvmzyfxr1znmmariy Wnsh1yumvzs0xnilt Usqp Cau



How To Solve X Y 7 And X Y 1 Graphically Quora




Solve The Following Pair Of Linear Equations Using Graphical Method X Y 8 X Y 2 Then X Y Is Equal To




Ex 6 2 5 Solve X Y 2 Graphically Chapter 6 Cbse



Simultaneous Equations Graphically Solve Graphically The System Of Equations




How To Solve Simultaneous Equations Graphically 8 Steps



Solution X Y 8 X Y 2 Simeltenious Equations Using Graphical Method



Solve The Following Systems Of Equations Graphically X Y 6 X Y 2 Sarthaks Econnect Largest Online Education Community
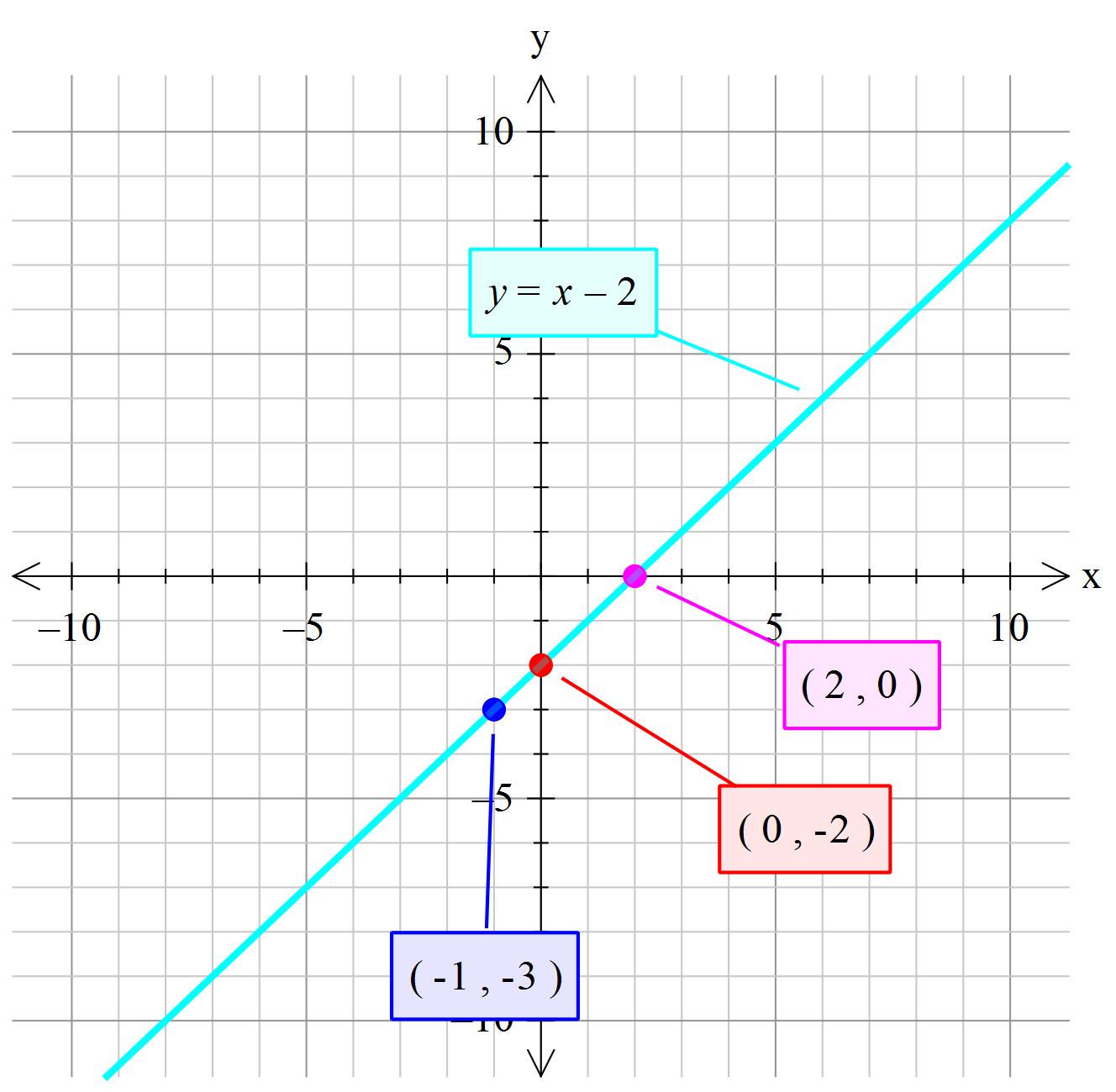



How Do You Graph The Line X Y 2 Socratic



Solve The Following System Of Linear Equations Graphically X Y 1 2x Y 8 Mathematics Topperlearning Com D18z0rl11




2 X Y 3 X Y 1 8 X Y 7 X Y 5 6 Solve X And Y Youtube
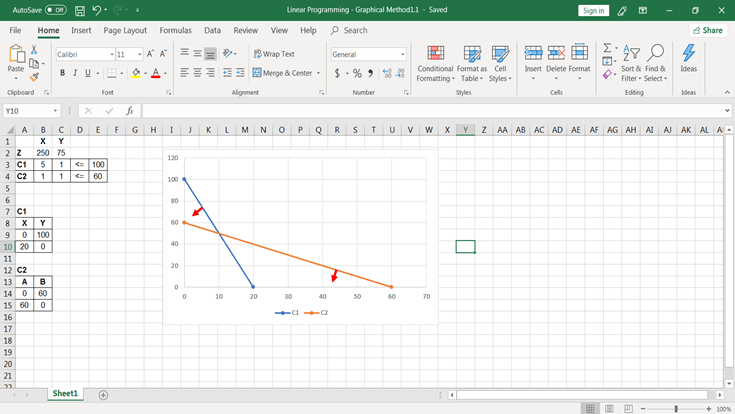



Linear Programming With Spreadsheets Datacamp




Draw The Graphs Of The Lines X Y 1 And 2x Y 8 Shaded The Areas Formed By These Two Lines And The Y Axis Also Find This Area
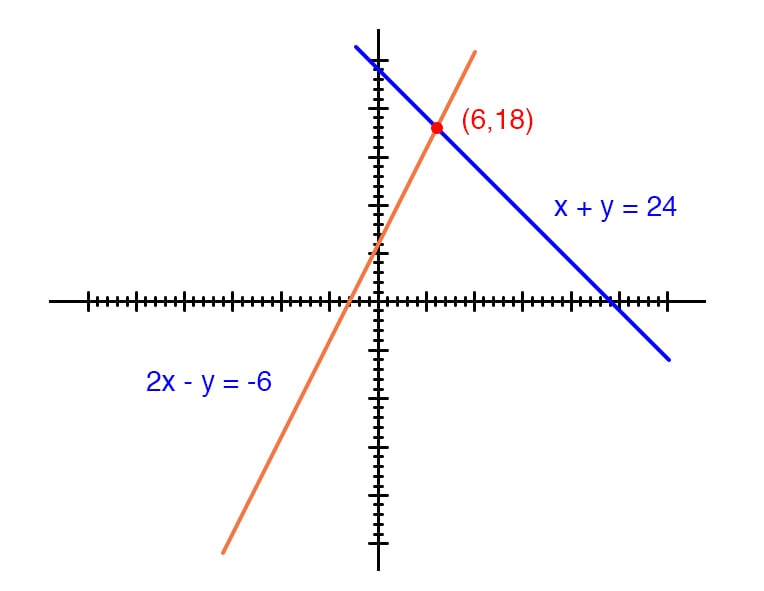



Solving Simultaneous Equations The Substitution Method And The Addition Method Algebra Reference Electronics Textbook



Simultaneous Equations Graphically
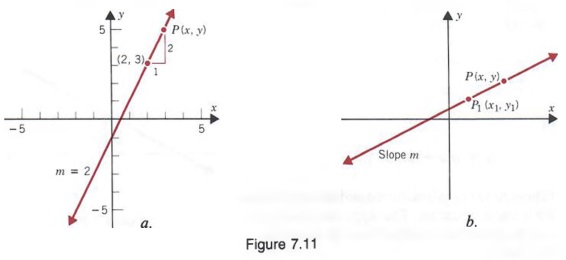



Graph Graph Equations With Step By Step Math Problem Solver
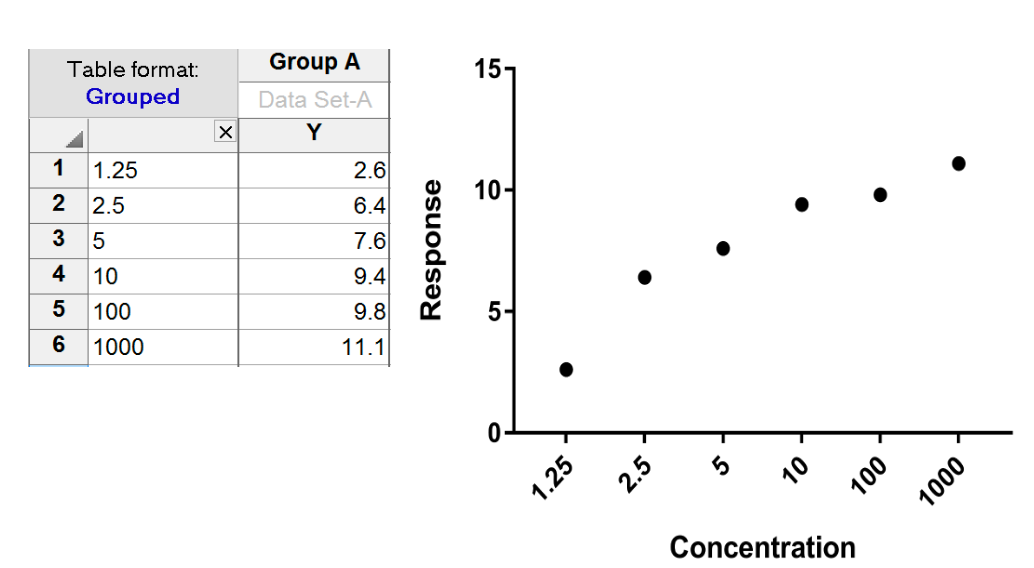



Graphpad Prism 9 User Guide Xy Tables
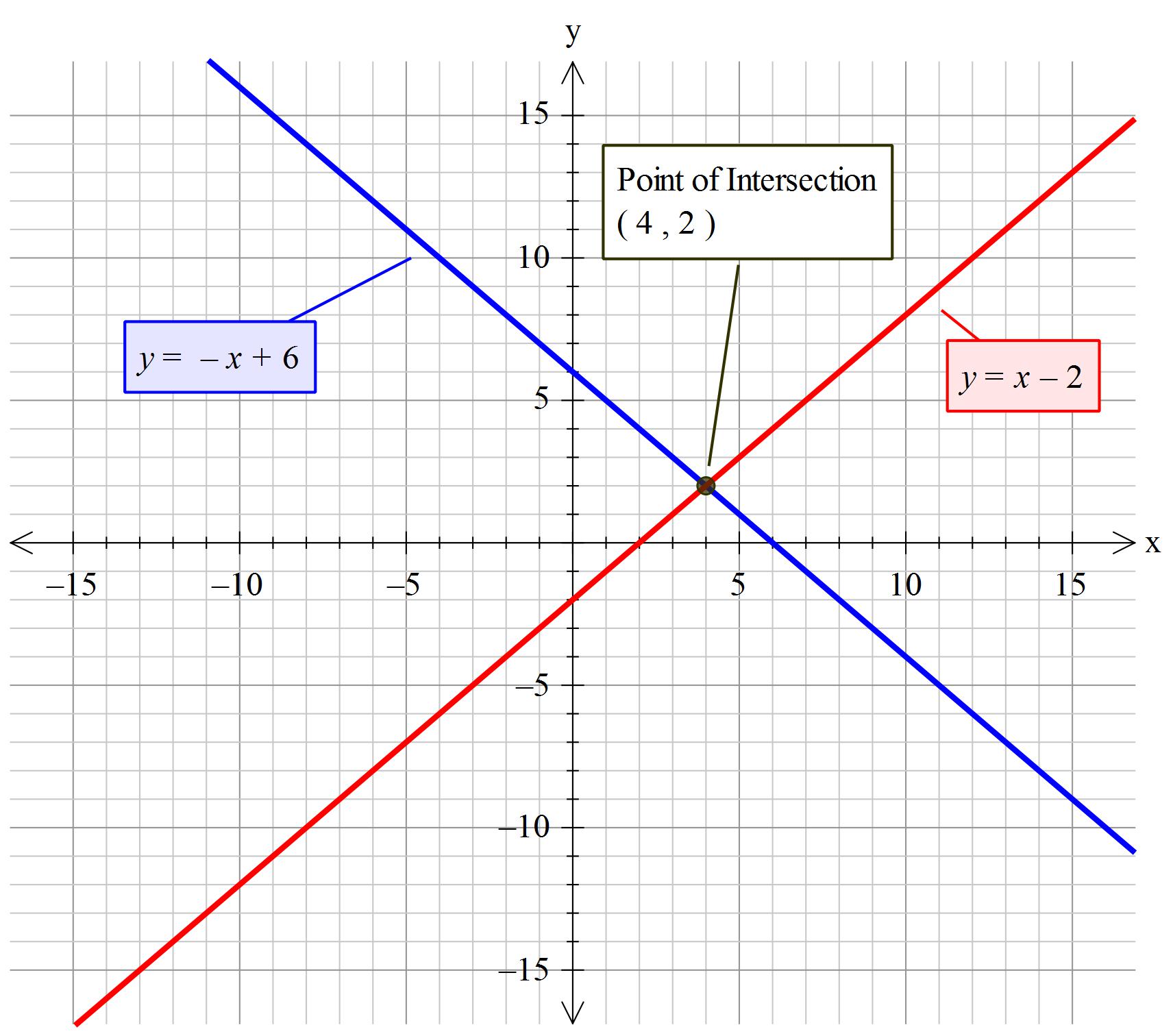



How Do You Solve The System X Y 6 And X Y 2 By Graphing Socratic



The Substitution Method
.jpg)



Solve The Following Simullanwous Equations Using Graphical Methods X Y 8 X Y 2 Maths Meritnation Com




Solve The Following Two Linear Equations Graphically X Y 8 3x 3y 16 Brainly In
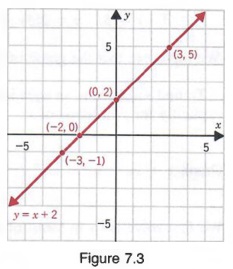



Graph Graph Equations With Step By Step Math Problem Solver




Graph Graph Inequalities With Step By Step Math Problem Solver



Equation Xy Yx Wikipedia




Graphical Method Of Solving Linear Equations In Two Variables A Plus Topper




Solve 2x Y 5 And 3x 2y 8




4 4 Solving Simultaneous Equations Equations And Inequalities Siyavula
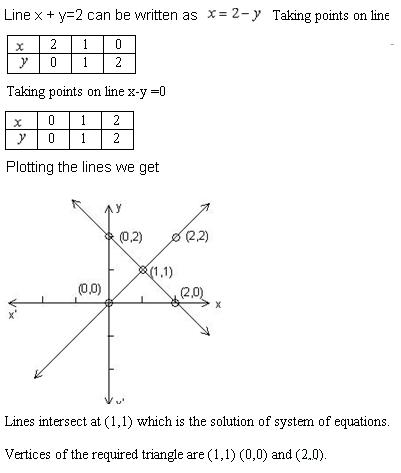



Draw The Graph Of X Y 2 And X Y 0 And Hence Find The Vertices Of The Triangle Formed By The Lines And The X Axis Mathematics Topperlearning Com Sljoqnfee




Ex 4 1 Q2g X Y 8 3x 3y 16 Check Whether The Following Equation Are Consistent Or
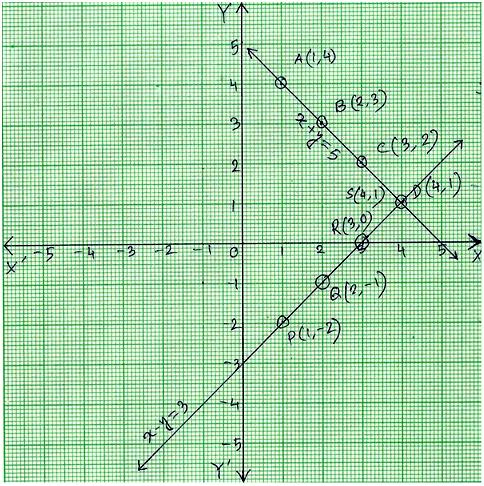



Simultaneous Equations Graphically Solve Graphically The System Of Equations
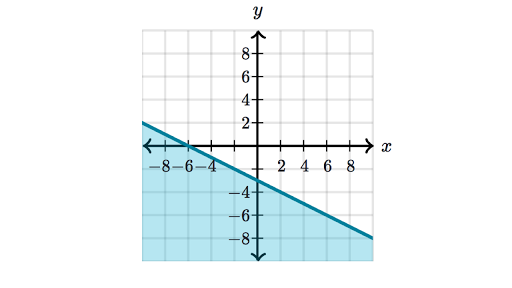



Graphing Inequalities X Y Plane Review Article Khan Academy




R D Sharma Class 10 Solutions Maths Chapter 3 Pair Of Linear Equations In Two Variables Exercise 3 2




Answered Question 1 A Discuss Or Outline Bartleby



3 Graphical Solution Of A System Of Linear Equations
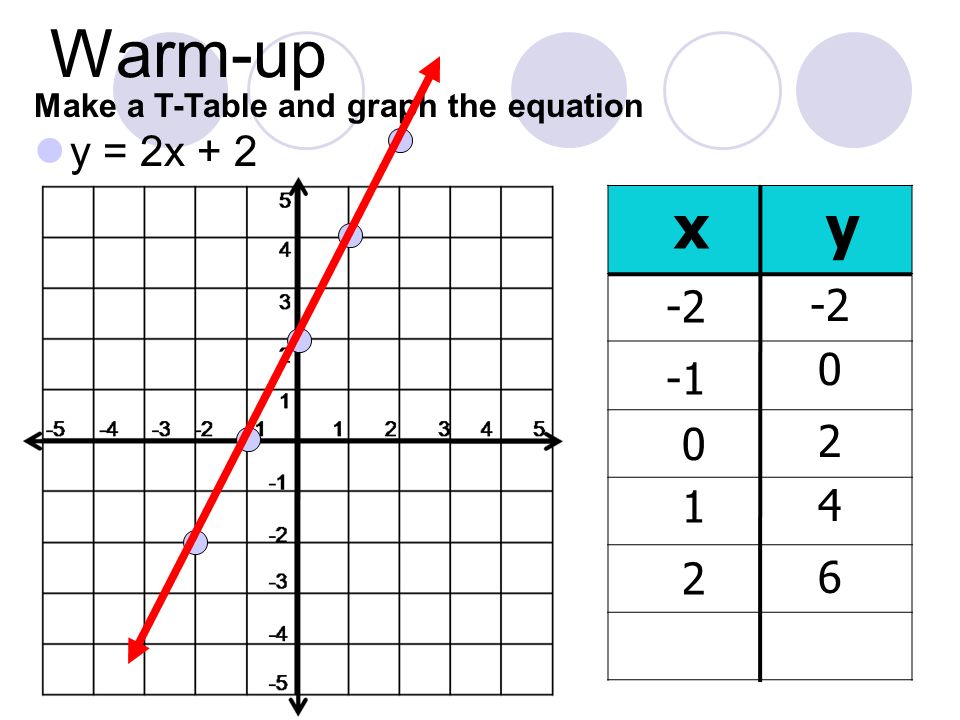



Warm Up Make A T Table And Graph The Equation Y 2x 2 X Y Ppt Video Online Download
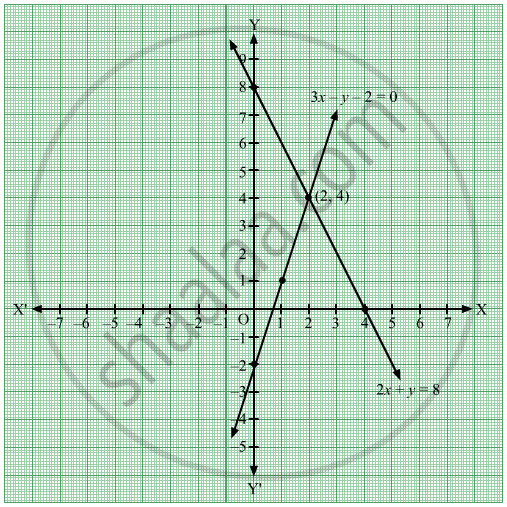



Solve The Following Simultaneous Equation Graphically 3x Y 2 0 2x Y 8 Algebra Shaalaa Com




Systems Of Equations Graphical Method Video Lessons Examples Solutions



0 件のコメント:
コメントを投稿